Les
mémoires associatives - Architecture
du réseau
- Le
principe
- L'algorithme
Modification
de la structure du réseau
Mise
en place d'une couche de sortie récurrente
Mise
en place d'une couche de sortie non-récurrente
Modification de la structure du réseau
Les
mémoires associatives Architecture
du réseau Le
principe L'algorithme
Modification
de la structure du réseau
Mise
en place d'une couche de sortie récurrente
Mise
en place d'une couche de sortie non-récurrente
L’algorithme d’Hopfield essaye de se rapprocher d’un exemple appris. Pour notre part, on souhaiterait donner une entrée à l’algorithme et récupérer uniquement une sortie qui n’a pas obligatoirement la même taille que l’entrée. On est donc obligé de modifier sensiblement l’algorithme afin de donner une entrée de taille n retournant une sortie de taille m.
On peut aussi essayer de changer quelques règles relatives à la structure du réseau au risque de perdre les critères de convergence.
Modification
de l'architecture du réseauHormis les paramètres de désapprentissage, deux autres paramètres importants peuvent subir des modifications :
L'auto-activation
du neurone
Le modèle de base du réseau de Hopfield est le modèle de Ising. Les atomes tentent de prendre la polarité du champ ambiant. Cette polarité ne concerne que les liaisons entre les atomes. En tenant compte de l’auto-activation du neurone, on prend en considération de façon forte la polarité du système. En effet du fait de la règle d’apprentissage, les neurones auront une auto-activation maximale (correspondante au nombre d’exemples).La moyenne de ces activations donnera donc la polarité ambiante au niveau de tout le réseau. Les modifications locales interviendront grâce aux poids sur les connexions (interactions). Le critère de convergence n’est plus vérifié avec cette hypothèse. Malgré tout, les tests ont permis de monter une convergence dans la majorité des cas.
Modification
des poids Synchrone ou Asynchrone ?
Le réseau de base préconise une modification des activations de manière asynchrone. Pourquoi ne pas donc considérer une modification des activations soudaine de façon synchrone. C’est à dire qu’à ce niveau l’activation des neurones ne dépend que de l’état précédent et plus de l’état en cours, contrairement à la modification asynchrone qui dépend à la fois de l’état courant et précédent.
Là aussi, le caractère asynchrone du réseau ne satisfait plus les critères de convergence sûre. Cependant on arrive à converger la grande majorité des cas (quasiment toujours). Le problème semble apparaître dés que l’on associe le caractère synchrone avec la non auto-activation du neurone. En effet ce mode converge très rarement, mais c’est le seul. Le but de ces modifications de mode de fonctionnement est bien sûr d’essayer d’améliorer le taux d’erreur en généralisation (sur apprentissage).
Mise
en place d'une couche de sortie récurrenteL'architecture du réseau n'est pas fondamentalement modifiée. La différence intervient au niveau de la phase de généralisation.
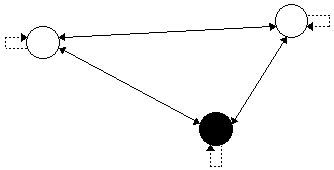
Architecture du réseau (en noir une sortie)
La phase d’apprentissage est strictement la même. Par contre, la généralisation est un peu modifiée. Au cours de la phase de généralisation par définition, on ne connaît pas la sortie. On initialise donc les entrées puis on calcule les sorties en fonction des entrées. La récurrence peut donc être lancée maintenant.
Algorithme
Mise
en place d'une couche de sortie non-récurrenteL’architecture subit ici des modifications importantes dans le sens ou les sorties ne sont plus récurrentes et n’ont plus de relations entre elles.
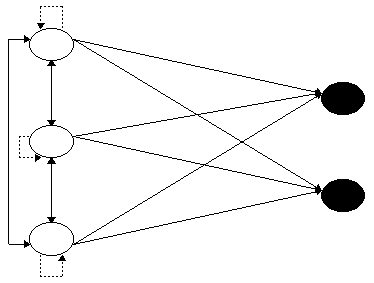
En noir les neurones de sortie (non-recurrents)
Au cours le la phase d’apprentissage, les connexions venant des neurones d’entrées vers les autres neurones sont modifiés. Par contre, les neurones de sortie n’ont aucune connexion allant vers un autre neurone. On isole ainsi la zone d’entrée et de sortie. Le principal changement apparaît dans le calcul des entrées à un neurone de la couche de sortie.
Algorithme
Mise
en place de sorties compétitivesOn calcule les sorties puis on ne garde activée que la sortie dont l’entrée totale est la plus grande et supérieure à 0. On peut donc se retrouver dans le cas je ne sais pas ou aucun des neurones n’a pu être activé. La raison de cette sortie compétitive réside dans la structure des classes de sortie. En effet elles sont contradictoires. C’est à dire que l’on ne peut pas avoir la sortie 1 activé avec la sortie 3.(Par exemple vote démocrate et républicain est incompatible)Une sortie est donc activée à la fois. Les autres restent à l’état 0 (ou -1).
L'algorithme est identique au cas précédent et peut même être appliqué à un ensemble de sorties récurrentes.
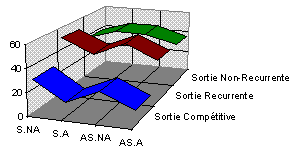
Variation de l'erreur sur la base Lenses en fonction de l'architecture
On remarque bien l’intérêt d’un tel découpage des sorties sous une forme compétitive. Les résultats sont considérés avec un désapprentissage de -0.01 de force en une seule passe.
Extension
des basesLa première solution proposée pour augmenter les résultats est bien sûr de réaliser une troncature préalable des bases. On élimine alors les cas qui créent des oublis dans le réseau. (Exemple du 8 et du 9 en reconnaissance). Les résultats s'améliorent très fortement grâce à un, découpage judicieux des données à faire apprendre au réseau.
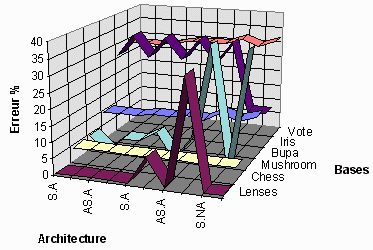
Résultats sur base tronquée en réseau à compétition
Vote en base complète donne une erreur légèrement inférieure. Il est donc important d'effectuer un très bon découpage des bases avant l'apprentissage.
Le paramètre A (Charge du réseau) est souvent très grand, du moins nettement supérieur à 0.14. D’ou l’idée de coder différemment la base. On peut par exemple dans un premier temps coder un 1 par 1 1 1 1 1 et un 0 par 0 0 0 0 0. Ainsi, on augmente le nombre de neurones et on diminue par la même occasion le paramètre A. Les résultats sont identiques que précédemment. Cela peut s‘explique par le fait que ce changement multiplie par x la force d’une classe quelconque. Les entrées totales au niveau des sorties sont donc toujours identiques à un facteur multiplicatif x prés.
D’ou l’idée de coder de façon aléatoire les entrées. C’est à dire que l’on prend une entrée et l’on étend la valeur booléenne 1 par 1 0 1 0 par exemple (aléatoire) et donc 0 par 1 0 1 0 (le complémentaire). De cette façon, on élimine le problème précédent. Cependant, les résultats restent les mêmes dans le cas d’un réseau de Hopfield à sorties compétitives.
Retour
à la page principale.