Les réseaux de Neurones

Le Réseau de Hopfield

Modification de la structure du réseau

Mise en place d'une couche de sortie récurrente

Mise en place d'une couche de sortie non-récurrente

Mise en place de sorties compétitives

Extension des bases

Le modèle de Hopfield fut présenté en 1982. Ce modèle très simple est basé d'une part sur le modèle des verres de spin de Ising mais aussi sur le principe des mémoires associatives. C'est d'ailleurs la raison pour laquelle ce type de réseau est dit associatif. Outre un intérêt pratique, ce réseau admet une analyse théorique précise et complète. Il a par ailleurs contribué à relancer les recherches sur les réseaux de neurones.

Les mémoires auto-associatives

Dans un mémoire informatique classique, une information est retrouvée à partir d'une clé arbitraire. Par opposition, une donnée entreposée dans une mémoire associative est accessible à partir d'informations qui lui sont associées.

La fonction d'une mémoire associative ressemble beaucoup à celle d'un filtre dont le but est de restituer une information en tenant compte de sa perturbation ou de son bruit. L'information doit alors se rapprocher d'une information apprise ou connue. Si les mémoires associatives restituent des informations qu'elles ont apprises à partir d'entrées incomplètes ou bruitées, il existe aussi des mémoires hétéro-associatives qui en plus peuvent associer plusieurs informations entre elles.

Un exemple d'associateur linéaire

Considérons un ensemble de couples (objet, numéro). On stocke l'ensemble de ces couples et on désire ensuite récupérer le numéro correspondant à un objet donné. Il est sûr que ceci n'est pas très complexe sauf peut être si l'on désire aussi récupérer un numéro à partir d'un objet voisin ou mal orthographié. Dans ce cas, la méthode doit s'arranger pour nous fournir le numéro correspondant au nom d'objet le plus proche.

Par exemple: (FIL, 301) (VIN, 198) (FAN, 512)

Si on fournit FIL, l'algorithme doit nous fournir 301. De même si on demande le numéro de PAN, il devra retourner 512. En effet, PAN est plus proche de VAN que de FIL ou VIN.

On a donc en fait une population de 8 noms:

FIL , FIN, FAN, FAL, VIL, VIN, VAN, VAL

On associe une distance de Hamming, il suffit alors de compter le nombre de lettres différentes: la distance entre FIL et VIL est de 1, la distance entre VIL et VAN est de 2 et la distance entre FIL et VAN est 3. En prenant une forme un peut géométrique, il suffit de placer les lettres dans une sorte de repère.

F (0,0,0) / I(1,0,0)

A (0,1,0) / N(1,1,0)

L (0,0,1) / V(1,0,1)

Il est possible de calculer une fonction qui à chaque entrée fournit exactement le numéro correct. On place alors nos trois noms d'objets dans le repère. Les coordonnées sont alors: FIL(0,0,1), FAN(0, 1, 0) et VIN(1,0,0). Une formule simple du type 3*x+2*y+1*z nous fournit alors le numéro (ici 1 2 3, ...).

De façon plus mathématique:

Soit (x1, y1), ..., (xL, yL) nos L exemplaires.
Si les vecteurs (x1, ..., xL) sont orthogonaux, on peut utiliser une fonction f(X') = y1 x'1 + ... + yL x'L, qui fournit pour X' = x1 la valeur y1.
Si on prend une valeur proche de l'un des xi, par exemple xi + delta, alors le système fournira f(xi + delta) = yi + f(delta) qui sera donc proche de yi.

Le réseau de Hopfield utilise cette propriété d'association linéaire.

Architecture du Réseau

Les réseaux de Hopfield dont des réseaux à rétroaction et à connexions symétriques. Les sorties sont fonctions des entrées et du dernier état pris par le réseau. Le principe général se rapproche beaucoup du modèle des verres de Spin de Ising.

Le modèle de Ising

Le modèle de Ising est en fait un modèle très simplifié des interactions magnétiques entre atomes. Dans ce modèle, chaque atome est décrit par la direction de son moment magnétique dont les valeurs sont limitées à -1 et 1. Chaque atome va ajouter une contribution au champ magnétique ambiant et de ce fait influencer ses voisins.

Si l'on note par Si le spin de l'atome i et Jij l'effet de l'atome j sur i, le modèle prévoit que la contribution hi de l'atome i au champ magnétique est la suivante:

Avec N le nombre d'atomes du système et en tenant compte de l'hypothèse très importante de symétrie Jij = Jji, et de non auto-activation, Jii= 0.

Dans un tel système, 2^N états sont possibles. Pourtant, certains de ces états sont plus probables et d'autres fortement improbables. En effet, un atome qui est de spin contraire au champ ambiant est instable. Il ne peut donc pas rester longtemps dans cet état. Une étude précise de ce comportement peut être effectuée après l'étude de l'énergie du système. Dans ce cas, l'énergie E décrit la somme des interactions entre les spins des atomes et l'effet de leurs champs magnétiques.

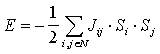
Dans la mesure où certains des états stables du système ont une énergie non négligeable, et où les interactions entre atomes peuvent être relativement variées, le modèle de Ising permet donc l’étude des systèmes frustrés et désordonnés.

L'architecture de base du réseau

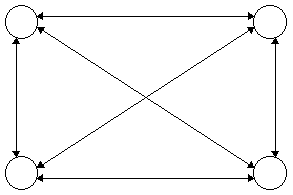
Les neurones de Hopfield sont discrets et répondent à une fonction seuil. Pour des commodités d’utilisation, on considère une fonction seuil très simple :

1, si x > 0

F(x) =

-1, sinon

Le réseau est complètement connecté, et les connexions sont symétriques.

Les valeurs d’entrée sont binaires (-1, 1) mais peuvent être aisément remplacées par les valeurs binaires usuelles (0, 1) en utilisant une simple transformation. A_(-1,1) = 2.A_(0,1) - 1

Le principe

Le réseau de Hopfield est l’un des réseaux les plus simples en particulier grâce à un apprentissage facile à mettre en oeuvre. Ce n’est qu’au cours de la phase de test que les problèmes les plus importants apparaissent.

L'apprentissage

La règle d’apprentissage proposée par Hopfield est basée sur la règle de Hebb. La règle de Hebb consiste à forcer les poids des liaisons entre les neurones actifs au même moment. Par contre, les poids seront diminués si les neurones sont dans des états contraires. Dans le cas de Hopfield, cette règle est légèrement étendue si l’on considère que deux neurones dans l’état -1 sont actifs. La règle de modification des poids devient donc:

P représente le nombre de patrons ou d'exemples

On remarque que la phase d’apprentissage est immédiate en calculant directement les poids à l’aide de cette fonction. C’est d’ailleurs l’un des seuls réseaux qui permet un calcul aussi simple et analytique des poids.

La généralisation

C’est maintenant que le problème se complique. Les poids ont été modifiés au cours de la phase d’apprentissage et ne seront plus modifiés. On présente alors le vecteur d’entrée au réseau. Ce dernier calcule la sortie correspondante et la ré-injecte à l’entrée. On itére le processus jusqu'à temps que l’entrée à l’étape t et la sortie correspondante (entrée de l’étape t+1) soient identiques. C’est à cause de ce processus que le réseau de Hopfield est classifié dans les réseaux récurrents. La règle de changement d’état est la suivante :

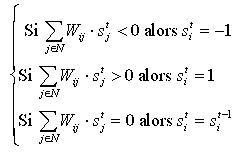
Maintenant, il faut être sûr de converger. Qu’elles en sont donc les conditions ?

Hopfield a démontré d’une part que son réseau évolue forcément vers un point fixe si il est en mode asynchrone, mais aussi l’existence d’une fonction de Lyapunov (équivalente à la fonction d’énergie de Ising) pour le modèle:

On peut facilement démontrer que cette fonction décroît avec l’évolution du réseau. En effet, supposons que l’on recalcule l’activation du neurone i. Ce neurone ne change d’état que si :

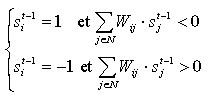
Supposons que s_i^t-1 = -1. Si le neurone ne change pas d’état, l’énergie demeure inchangée. En revanche si son activation passe à 1, la différence d’énergie résultante est :

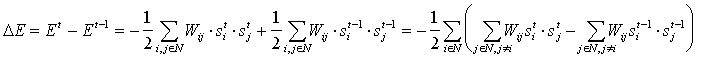
Sachant que seul le neurone i a changé d’état l’expression devient alors :

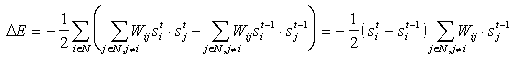
Or par hypothèse on a :

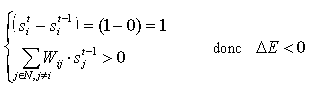
Ainsi, l’énergie du réseau de Hopfield ne peut que décroître, cela garantit donc la convergence du réseau à des points fixes.

Capacité du réseau

Après la phase d’apprentissage et après une période d’itérations plus ou moins grande, le réseau arrive à un point de convergence qui n'est pas systématiquement un état appris par le système mais parfois un état poubelle. Définissons alors le taux de chargement du système: A = P / N. (P nombre de Patrons; N nombre de Neurones).

D’après l’étude de Hopfield , on peut repérer 3 zones :

Lorsque peu d’états sont appris, ils sont entourés de larges bassins d’attraction. Ils peuvent donc facilement être restitués sans erreur à partir d’un état qui leur est relativement distant. Cependant, les états désirables sont aussi accompagnés d’attracteurs parasites. Ces états deviennent progressivement moins stables avec l’augmentation de la charge, et deviennent instables à un taux de chargement de 0.03.
Au dessus de ce taux, les bassins des états appris sont beaucoup plus petits, et les patrons appris ne peuvent plus être retrouvés sans erreur. L’erreur est d’environ 1.5% à A=0.14
Au delà de ce dernier taux, les capacités du réseau peuvent disparaître On appelle ce phénomène l’oubli catastrophique.

Pour remédier un peu aux effets attracteurs des états stables indésirables, on peut utiliser une phase de désapprentissage. Cette phase consiste à tirer un patron au hasard et à le présenter au réseau. Il y a de très forte chance qu’il converge vers un état stable indésiré. On opère alors l’opération inverse de l’apprentissage en diminuant les poids des connexions sur les neurones co-activés au même moment. Bien sûr, il faut que la force du désapprentissage ne soit pénalisant que pour les états indésirables.