Les réseaux de type Auto-organisateur de Kohonen sont très utilisés à l’heure actuelle. En effet, ce réseau peut être considéré comme dynamique dans le sens ou il a tendance à créer ou détruire des neurones. De plus ces réseaux fonctionnent dans leur très grande majorité dans un mode non supervisé. Il est donc relativement difficile de lui faire apprendre nos bases. Cependant, il n’est pas exclus qu’une étude plus approfondie de ces réseaux puisse donner des résultats intéressants dans l’extraction de propositions logiques par exemple.
Principe
du réseau concurrentiel
L'architecture
de base
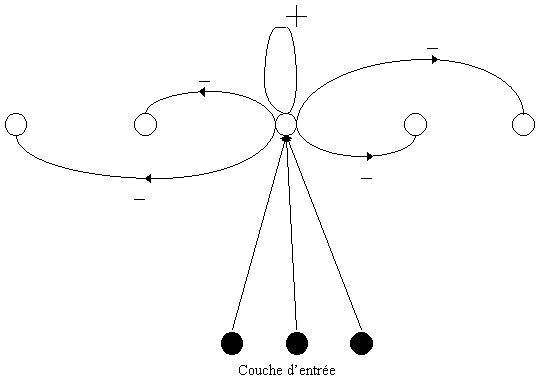
Voici une exemple assez simple d'architecture compétitive.
Il y a peu de conditions à remplir pour qu'un réseau soit compétitif :
On utilise alors le réseau de façon très simple en présentant une entrée qui va provoquer des réponses des neurones de la couche suivante. C’est à ce niveau que l’on peut lancer une compétition entre les neurones. Cette compétition aura pour but d’élire un neurone vainqueur. Il ne reste plus qu’à définir ce qu’est un neurone vainqueur.
Dans le cas d’un apprentissage supervisé, on peut considérer par exemple le neurone le plus activé mais aussi le neurone qui minimisera l’erreur avec la sortie souhaitée. C ‘est en général ce neurone qui va subir une modification de ses connexions bien que cela ne soit pas une règle générale. Dans un cadre non supervisé, on ne possède pas de structures connues de type (entrée, sortie). La règle de compétition ne peut donc pas être la même que précédemment. On peut alors imaginer des règles du type le neurone le plus activé l’emporte. Il arrive assez souvent que l’on considère le neurone se rapprochant le plus du vecteur d’entrée comme neurone gagnant. Dans ce dernier cas, on peut citer par exemple une minimisation de distances, ... .
Cependant, là ou la règle de Hebb a la propriété de trouver automatiquement des corrélations entre neurones, les règles d’apprentissage compétitives ont plutôt tendance à pousser à une sélection parmi les exemples. Cette capacité de découvrir automatiquement des catégories dans un ensemble de données fait de ces réseaux des techniques efficaces de classification.
Un apprentissage
compétitifLe principe d’un apprentissage compétitif est en général de favoriser le vainqueur. On peut considérer que favoriser le neurone gagnant peut être de le rapprocher du vecteur d’entrée à qui il doit sa victoire. De ce fait, les chances de victoire de ce neurone quand on représentera cette entrée seront plus élevées. Par contre, il sera peut être plus pénalisé au niveau d’entrées plus éloignées.
C’est de cette simple constatation que les réseaux que nous allons étudier tirent leur nom : réseaux auto-organisateurs. En effet, on apprend à ce neurone à gagner pour un petit nombre d’entrées semblables. Par conséquence, il va agir comme un détecteur de ce type d’entrées. Ce réseau à donc des capacités de classification.
Essayons dans un premier temps de présenter une règle d’apprentissage de base que nous allons modifier par la suite pour le besoin des réseaux de Kohonen.
L’apprentissage suppose deux phases :
On recherche donc le neurone i qui a été soumis à l’activation la plus forte et on le désigne comme vainqueur :
La modification des poids peut simplement consister à ajouter, ceci à un coefficient près, le vecteur d’entrée à l’ancien vecteur de poids correspondant du neurone vainqueur.
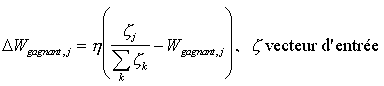
Par contre, on peut, ne pas toucher (de la même façon) aux autres neurones, ou modifier en même temps les neurones voisins en introduisant une notion de distance entre les neurones. Pour résumer, cette technique contribue à diminuer l’angle entre le vecteur d’entrée et les poids des neurones gagnants.
Les
cartes Topologiques de KohonenUne carte de Kohonen est un réseau où les unités ne sont connectées qu’aux entrées. Toutefois, des contraintes topologiques sont utilisées pour former des inhibitions. Ces inhibitions sont par ailleurs intégrées dans le poids des connexions liant les neurones aux entrées. Des versions totalement connectées sont également possibles. Dans ce cas, chaque neurone est connecté à tous les autres et les poids des connexions reflètent rigoureusement les inhibitions induites par la topologie.
Cette structuration va aussi lier les neurones ensemble sur une surface élastique. Il en résulte donc que le comportement des neurones varie graduellement d’une région à l’autre de la carte. Ce type de structuration est fréquemment observé dans le cerveau ou on retrouve souvent des cartes topologiques.
L’intérêt majeur des cartes topologiques est de représenter sur un petit nombre de dimensions la structure présente dans des données de haute dimensionnalité. C’est donc une méthode d’analyse de données performante.
L'architectureLe réseau de Kohonen est essentiellement composé d’une couche d ‘entrée et d’une couche compétitive. La structuration topologique de la carte provient d’une mesure de distance d définie sur les neurones du réseau. On défini ainsi un voisinage du neurone. On peut donc modifier les poids des neurones voisins par la même occasion.
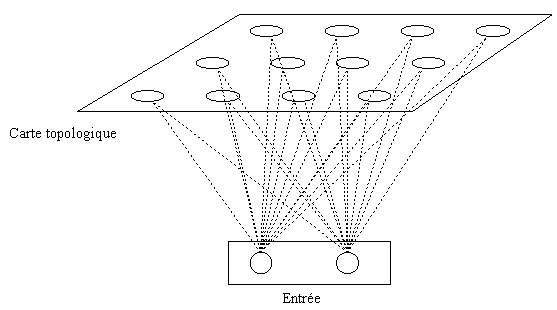
ApprentissageDés que l’on a obtenu le neurone vainqueur, on modifie les poids en fonction de la distance du vecteur à ce neurone.
Maintenant, il faut faire en sorte que plus un neurone est loin du vainqueur, plus faible sera sa correction. Par conter si le neurone est très proche, il sera lui aussi modifié en conséquence.
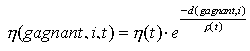ou
p(t) représente un voisinage qui décroit avec le temps.
On peut aussi simplifier quelque peu l’apprentissage en considérant :
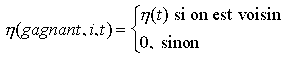
Dans notre algorithme, on va mélanger les deux règles . On peut alors utiliser une formule proposée pat Kohonen :
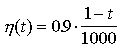
Les vecteurs d’entrée s’obtiennent en tirant aléatoirement des couples de valeur dans la structure que l’on veut cartographier avec Kohonen. Par exemple, pour un carré en deux dimensions, on aura deux poids x et y. On tirera donc aléatoirement des couples (x,y) à l’intérieur du carré, les neurones vont élire le vainqueur comme étant le plus proche de ce point. On va donc dessiner une carte précise ou un maillage de cette forme.
AlgorithmeL’algorithme présenté ici fait intervenir plusieurs paramètres que l’on n’a pas présenté au début mais qui s’avèrent utiles à l’évolution du réseau. De plus la carte présentée ici est en 2D. C’est la raison pour laquelle on a un poids x et y représentant la position spatiale du neurone.
ParamètresLes paramètres utilisés sont:
RésultatsVoici un exemple de résultats sur plusieurs types de formes.
Un carré
Un Triangle
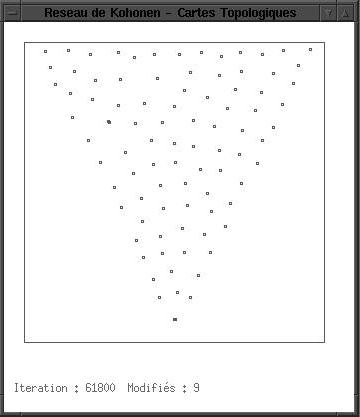
L'évolution pour 1/4 de disque :
Problème
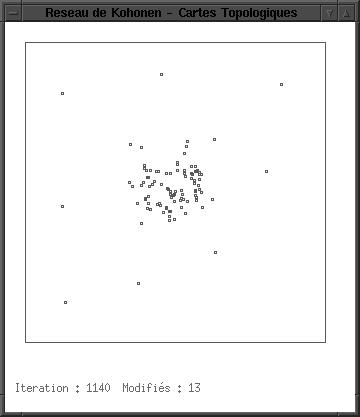
du voyageur de commerceContrairement à l’exemple précédent, on ne va pas chercher à auto-organiser la carte. L’apprentissage consiste ici à faire déplacer topologiquement les neurones pour les faire coïncider avec l’espace réel. Le réseau va rester sous une forme compétitive mais les règles d’apprentissage et l’architecture vont être modifiés.
L'architectureOn a toujours un modèle à deux couches :
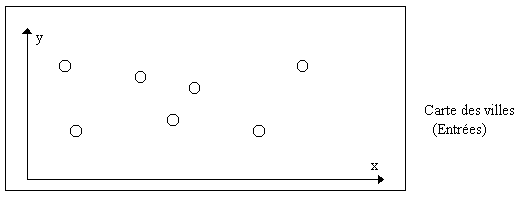
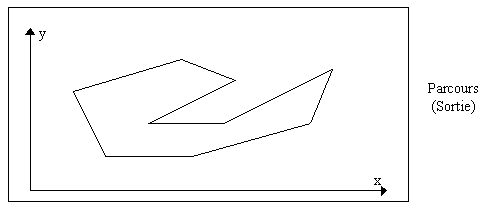
La particularité de ce réseau est aussi d’avoir une évolution dynamique des neurones. Non seulement les neurones bougent sur la carte jusqu'à tomber sur une ville, mais ils peuvent aussi disparaître si ils partent sur une mauvaise direction ou se créer si il y a trop de villes à visiter dans cette direction.
L'apprentissageL’apprentissage est relativement simple. Comme précédemment on tire une ville (couple (x,y)). On recherche alors la « balise » ou neurone le plus proche de la ville. Ce sera le neurone vainqueur. La nome utilisée est bien sûr une norme 2 car on est en 2D.
On déplace alors dans un second temps la balise vers la ville. Comme dans le cas de la carte topologique, on s’arrange pour aussi tirer les voisins vers la ville sélectionnée. On s’arrange seulement pour que son attraction soit moins forte.
La force de cette attraction doit être forte au départ pour permettre aux neurones de s’étendre puis doit s’affaiblir au fur et à mesure pour stabiliser le neurone autour des villes.
Dés que toutes les villes ont attiré un neurone vers eux, on regarde quels neurones n’ont pas été utilisés depuis un certain nombre d’itérations. Ces balises ne sont donc pas assez proche d’une ville. On peut donc essayer de le rapprocher d’une ville ou le détruire. La dernière solution est la plus logique.
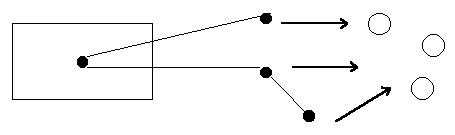
En noir, on représente une balise et les gros cercles sont des villes. On se rend bien compte que la balise encadrée n’est plus nécessaire et pénalise le réseau. On peut considérer aussi qu’il y a trop de villes pour le nombre de balises à proximité.
Il arrive alors que des balises soient attirées par plusieurs villes (puisque certaines ne sont pas attirées). Cela veut dire que la balise est proche de plusieurs villes et est le seul à en être aussi proche. Il faut donc lui amener de l’aide en créant des balises autour de lui. On crée autant de balises qu’il a été activé.
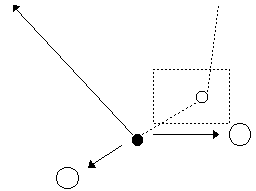
En encadré la balise à créer pour pouvoir établir un trajet vers les deux villes. Sinon, le neurone aurait osciller très longtemps entre les deux villes sans pouvoir se décider.
On passe donc par des phases de création et destruction de neurones. Il peut donc y avoir plus ou moins de balises que de villes.
Le démarrage peut s’effectuer de plusieurs façons :
On a alors une convergence dès que
Cette méthode constitue une façon efficace de traiter un problème d’optimisation. Se reporter au livre de Kohonen pour plus de détails et des démonstrations plus mathématiques.
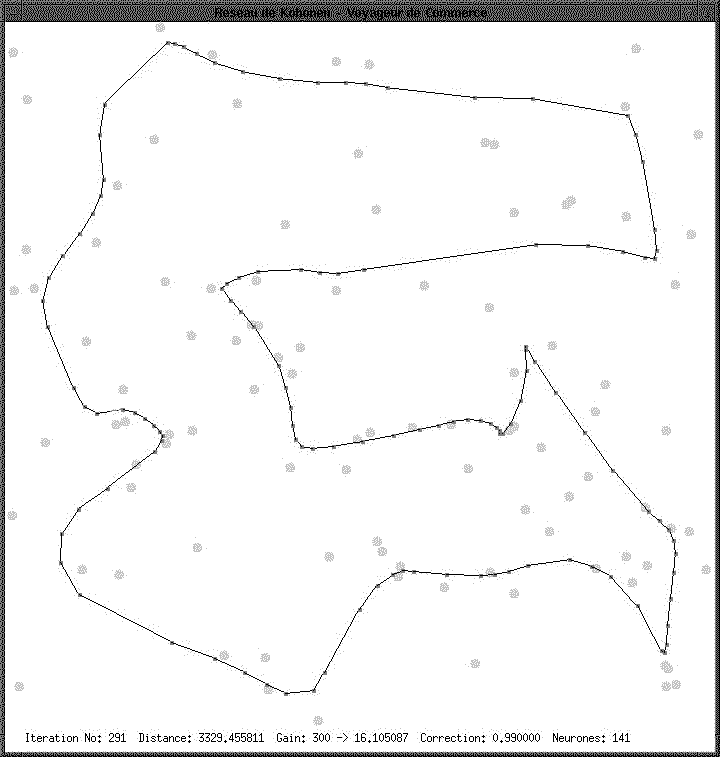
L'AlgorithmeRésultatsLes résultats semblent très corrects. Une valeur de gain forte entraîne une convergence rapide du réseau vers un parcours. Ce parcours n’est pas toujours le plus optimal que puisse sortir le réseau. Un gain faible au départ entraîne une convergence plus lente mais un meilleur résultat. Le paramètre de correction de ce gain est aussi très important, il détermine si le réseau va évoluer beaucoup très longtemps ou très peu de temps. C’est le facteur le plus important vers une bonne convergence.
Plus ce paramètre est proche de 1 meilleur sera le résultat, car le réseau aura eu le temps au début de beaucoup évoluer et de converger ensuite plus finement vers la fin.
Le gain initial est en général de 1 tandis qu’un bon coefficient de correction est de 0.99.
Ce réseau est un assez bon « optimiseur » du problème du voyageur de commerce.
Retour
à la page principale.
