Ce réseau a été inventé par Hecht Nielsen. Il n’a pas de caractéristique révolutionnaire nouvelle mais ressemble beaucoup plus à un assemblage de pièces venant d'autres réseaux. Une approche de ce réseau bien que limitée est assez intéressante au titre d’une introduction aux réseaux à compétition du type Kohonen. Le grand intérêt de ce type de réseau est d'effectuer des classifications et par extension de la reconnaissance.
L’algorithme de contre-propagation utilise une architecture proche du perceptron. On a en effet une couche d’entrée, une couche de sortie mais aussi une et une seule couche intermédiaire (bien que l’on puisse concevoir ce réseau avec plusieurs couches cachées).

L’originalité du réseau vient du fait qu’il mélange deux types d’apprentissage en fonction de la couche considérée.
Les règles de calcul des entrées à un neurone sont identiques aux autres réseaux. Cependant, la règle d’activation d’un neurone, et c’est la nouveauté est de type compétitive. C’est à dire que l’on va déterminer un neurone gagnant qui lui seul sera activé.
En effet, de manière interne, ce réseau effectue une classification. Ceci peut être intéressant pour la reconnaissance de formes. Il suffit de faire en sorte qu’au cours de l’apprentissage, on apprenne toutes les formes à reconnaître. Elles vont donc aller se nicher dans les neurones de cette couche. Il faut par conséquent prévoir assez de neurones dans cette couche.
Pour bien fixer l’utilité de ce réseau, considérons l’exemple suivant : A partir d’une image d’un missile, on veut connaître son angle d’inclinaison. On fixe alors en entrée la matrice des pixels représentant le missile. La couche de sortie pourra par exemple nous donner l’angle. La couche intermédiaire pourra alors servir à reconnaître des angles du type 0°, 45°, 90°, ... . On a donc autant de neurone dans cette couche que de catégories à classer.
![]() L'apprentissage
L'apprentissage
L’apprentissage s’effectue en mode supervisé. En d’autres termes, on présente au réseau des modèles du type (entrée, sortie). Les valeurs des poids des connexions de la couche intermédiaire et de sortie sont choisis aléatoirement. On entraîne en premier lieu la couche intermédiaire en présentant les exemples. Pour chaque exemplaire, on effectue alors une normalisation de l’entrée pour éviter une divergence du réseau:
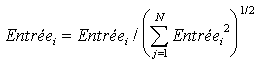
Pour chaque neurone intermédiaire on calcule l’activation totale du neurone. On répète le processus pour chaque neurone avant de modifier les poids selon une règle du type Widrow-Hoff. Cependant, on ne modifie pas le poids de toutes les connexions mais seulement les poids « du neurone gagnant », c’est à dire du neurone à la plus forte activation :
Wgagnant,i = Wgagnant,i + Alpha (Entréei - ti), t activation du neurone
Cette règle va avoir pour effet de rapprocher encore plus le vecteur des poids du vecteur d’entrée correspondant.
Pour arrêter cet apprentissage, on attend que
Dès que la couche intermédiaire est capable de placer un élément dans une catégorie, on peut procéder à l’apprentissage de la couche de sortie. On propage alors l’entrée vers la couche intermédiaire afin d’élire le neurone vainqueur. On ajuste alors les connexions de ce neurone vers la sortie à l’aide de la règle :
Wj,gagnant = Wj,gagnant + Beta (Sortiel-Wj,gagnant)
Cette phase se poursuit tant qu’un critère de convergence n’est pas atteint. Par exemple, on peut fixer comme critère, l’erreur entre la pondération et la sortie réelle est inférieure à un seuil (0.01, ...).
![]() La phase
de généralisation
La phase
de généralisation
On effectue tout simplement une propagation de l’entrée vers la couche intermédiaire afin d’élire un neurone gagnant. Ce neurone déterminé, on propage alors vers la couche de sortie.
Voici d’abord des résultats sur de la reconnaissance de forme. On apprend au réseau à reconnaître 4 formes représentant un missile en inclinaison. La sortie doit donc nous donner cette inclinaison. Par contre il est assez difficile de faire en sorte que le réseau apprenne les bases de données (Lenses, Mushroom, Vote, ...) car elles sont trop proches et bloquent la phase de convergence au niveau de la correction des poids. De plus, il faut sans doute faire en sorte qu’il y ait une catégorie par exemple. Cependant en diminuant la taille de la base on obtient des résultats.

Les données à apprendre

Le résultat en généralisation sur apprentissage
Cette méthode est relativement rapide. On peut peut-être l’utiliser pour la formation des propositions logiques.
Les paramètres utilisés sont :
Il serait intéressant de traiter plus en détail ce réseau car on peut éviter les oscillations qui s’opèrent souvent avec nos bases (formes trop proches et trop de cas d’apprentissage) en faisant une modulation des coefficients d’apprentissage. Par exemple, on peut partir de coefficients très gros puis les diminuer très progressivement ou faire l’inverse pour éliminer des cas de la base. Ce réseau est aussi extensible en propagation inverse, mais malheureusement, je n’ai pas pu trouver de littérature traitant plus en détail de cet algorithme.