Dans l'optique d'une amélioratio des résultats obtenus avec un réseau de type Hopfield, il semblait intéressant d'utiliser un réseau à la même architecture globale mais muni de règles d'apprentissage différentes. Le réseau présenté ici, bien que possédant un couche récurrente est classé dans les réseaux purement déductifs. De plus, il présente aussi l'avantage de définir directement des couches d'entrées et de sorties dans ses phases d'apprentissage et de généralisation.
L'Architecture
du RéseauL'architecture du réseau est fortement récurrente comme dans Hopfield. La couche intermédiaire est entiérement récurrente par contre, et c'est là la différence majeure, les couches d'entrées et de sorties ne le sont pas.
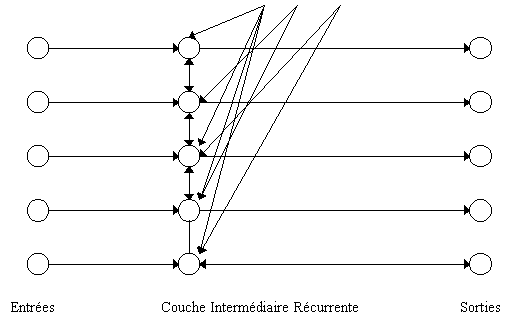
Pendant les calculs de propagation, il faut que chaque neurone utilise en entrée le même vecteur et non pas le vecteur modifié par les calculs comme pour Hopfield. C'est la raison pour laquelle on doit ajouter une couche d'entrée qui conserve donc la valeur d'entrée à appliquer à chaque neurone.
Le
PrincipeCe réseau a été conçu par James Anderson sous le nom de Brain in a Box afin d'étudier les fonctionnalités du cerveau humain. En d'autres termes, ce réseau essaye de modéliser un comportement psychologique. On essaye d'effectuer des raisonnements du type:
Socrate est un Homme
Les Hommes sont Mortels
Socrate est Mortel
Il suffit de lui apprendre les règles de base de ce raisonnement et le tour est joué. On peut aussi préciser que ce réseau est une certaine évolution de Hopfield. Il agit en effet comme un associateur linéaire avec un ensemble de liaisons supplémentaires qui essayent de corriger les interférences parasites des systèmes linéaires.
Le Calcul
de la SortieLe calcul de la sortie est basé sur le même principe que pour Hopfield mais avec des termes un peu plus complexes.
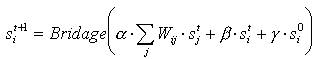
De bonnes valeurs de calcul semblent être a peu prés:
La Phase
d'ApprentissagePour réaliser la phase d'apprentissage, on initialise d'abord les poids à des valeurs faibles par exemple dans [-0.001, 0.001]. On présente alors les vecteurs d'exemples en entrée. On propage ainsi la valeur vers la couche intermédiaire. La propagation finie, on calcule la différence entre la valeur réelle de l'exemple en sortie et la valeur calculée. On obtient alors la valeur de correction des poids. On ré-injecte alors cette valeur calculée en entrée de la couche intermédiaire et on répéte le même processus.
Cette phase d'apprentissage est répétée un certain nombre de fois, fixe et déterminé à l'avance. Ce paramètre joue un rôle très important dans l'erreur d'apprentissage.
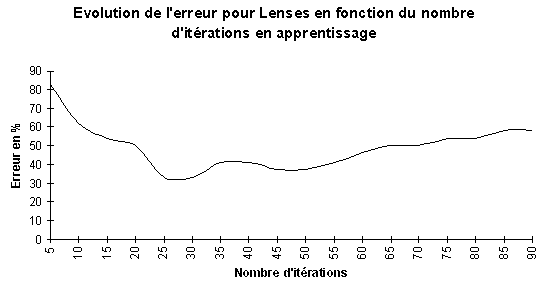
Un deuxiéme paramètre intervient de façon très prépondérante: le facteur d'apprentissage lors de la modification des poids. La règle de modification est une simple règle de Widrow-Hoff pondérée.
Wt+1ij=Wtij + Facteur_d'apprentissage.Erreuri.sj
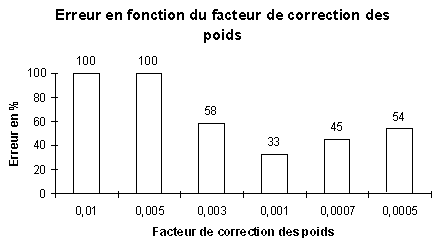
Enfin, l'initialisation aléatoire des poids doit se faire entre des bornes les plus faibles possibles pour améliorer la convergence.
La Phase
de VérificationLa phase de vérification utilise le même algorithme sans modification des poids (réseau statique). On serend très vite compte que les valeurs de sorties convergent rapidement vers les bornes (positive et négative). En effet, si la valeur d'apprentissage est forte, on dépasse rapidement la valeur limite et on diverge alors en très peu de temps vers l'infini. In ne faut pas oublier que le calcul d'une sortie utilise les paramètres (Alpha, Beta, Gamma) dont la somme est supérieure à 1. Cela favorise la multiplication, à chaque itérations de valeurs supérieures à 1 qui grossissent de plus en plus. C'est assez surprenant la première fois que l'on lance ce réseau.
Le codage
des Bases de DonnéesL'algorithme est à la base crée pour modéliser des phénomènes du type: A => B; B => C. O, peut par exemple avoir:
A: symptômes de la voiture
B: type de problème
C: solution
Le codage peut alors être:
On se rend compte qu'il faut trois états:
En effet, quand on apprend au réseau batterie à plat, on ne doit pas lui apprendre en même temps problème électrique. C'est quand on lui apprend A => B qu'il faut lui dire batterie à plat => problème électrique. On doit donc désactiver une partie des informations. On utilise de façon identique cette technique à trois ètats pour la généralisation en précisant cette fois qu'un 0 signifie une recherche de valeur (soit 1 ou -1).
On à donc clairement deux phases dans l'apprentissage. La premiére consiste à apprendre les entrées puis les sorties et enfin les sorties correspondantes aux entrées.
En réalisant deux programmes différents pour l'apprentissage on peut tester l'effet d'un mode entrée + sortie et un mode d'apprentissage d'une entrée puis d'une sortie, et enfin de l'entrée et de sa sortie correspondante.
L'AlgorithmeUne
idée de Structure de DonnéesOn peut modéliser un neurone de la façon suivante:
On réalise alors un tableau de nb_neurones structures neurone.Les neurones des trois couches sont décrits par la structure précédente. En effet le réseau est entièrement récurrent donc au cours des phases d’apprentissage et de généralisation il n’y a pas réellement de neurone défini (dans l’architecture) comme neurone d’entrée ou de sortie. L’entrée se déplace vers la couche intermédiaire (en récurrence) jusqu'à la sortie. Toutes ces couches ont donc la même taille et le même nombre de neurones. C’est pour cette raison que l’on utilise cette structure de codage d’un neurone. Seul la forme des bases à apprendre (présence ou non de 0) définie des zones d’entrée ou de sorties (ou plus).
L'AlgorithmeVoici l'algorithme procédant à un apprentissage des bases sous la forme directe A => B. En italique on repérera l'apprentissage des entrées et sorties seules.
RésultatsLes résultats avec un apprentissage découpé (entrée puis sortie et enfin entrée + sortie) ne semble pas donner de bons résultats vis-à-vis d'un apprentissage direct de la base qui doit être modifiée en conséquence (les 0 présents dans les bases initiales doivent être changés en -1). Il est à noter que cet algorithme peut être utilisé très simplement pour un cas A => B; B => C en créant les bases d'apprentissage sous la formej'apprends A puis B puis C et enfin A => B et B => C, en plaçant des 1 pour les valeurs activées, -1 pour les valeurs désactivées et 0 pour les valeurs inutilisées. Par exemple, pour apprendre uniquement électrique il faudra placer mécanique à 0 pour indiquer qu'il n'est pas appris.
On peut cependant considérer un algorithme strictement identique en supposant qu'une valeur non-utilisée doit être à -1 par défaut. Par exemple un ennui purement électrique peut supposer que la cause mécanique est à désactiver. Le fait d'utiliser une représentation sous cette forme est personnelle et n'est pas basée à priori sur l'algorithme présenté par Anderson. Les résultats sont pourtant loin d'être mauvais suivant la base utilisée dans cette configuration binaire 1 et -1.
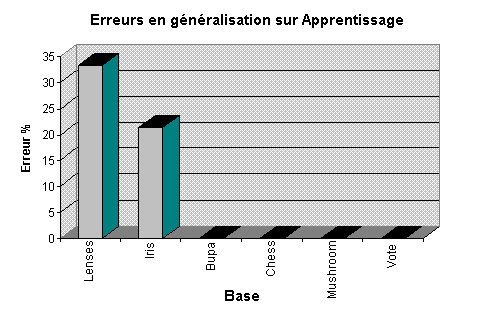
Les paramètres utilisés pour l'erreur minimale sont:
Sauf pour la base Iris, la force d'apprentissage (0.001) est de 0.0002 et le bridage à 1.15. Par contre je n'ai pas réussi à trouver de bons paramètres pour diminuer l'erreur avec la base Lenses.
Retour
à la page principale.
