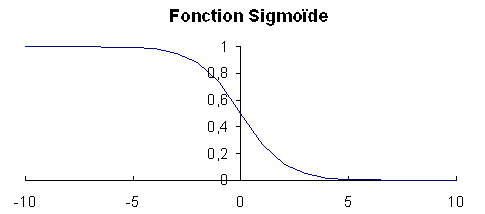
Les réseaux de Neurones

La rétro-propagation du gradient

Les réseaux mono-couche (couche d’entrée et/ou de sortie) peuvent être entraînés avec des règles d’apprentissage relativement simple. En contrepartie, ce genre de réseau est limité au calcul de fonctions très simples. D’ou l’intérêt de créer des réseaux plus élaborés, contenant par exemple des neurones cachés, c'est à dire des neurones qui ne sont ni de la couche d'entrée ni de la couche de sortie. Cependant, même si ces réseaux ont des capacités de calcul plus grandes, leur apprentissage ou l’attribution des poids des connexions devient très difficile. Les réseaux multil-couches comme par exemple le perceptron multicouche sont assez récents. Ce dernier utilise d'ailleurs l’algorithme de rétro-propagation du gradient pour effectuer la mise en place de la pondération du réseau.

L'architecture du réseau

Le réseau présenté ici présente les caractéristiques suivantes:

Il comporte une seule couche d'entrée.
Il comporte une seule couche de sortie.
Il peut comporter de une à plusieurs couches cachées.
Chaque neurone est uniquement relié à tous les neurones de la couche suivante.
On considère des neurones non biaisés.
La fonction de transfert est une sigmoïde.

f(x) = 1 / ( 1 + exp(x) )

Rappelons les formules de calcul pour un neurone. Considérons donc un neurone i de la couche intermédiaire k + 1. Il reçoit en entrée une somme pondérée fonction de l'état des neurones précédents. On effectue donc:

le calcul de la somme pondérée à l'entrée (somme pour tous les neurones de la couche k de l'activation du neurone j de la couche k multiplié par le poids de la connexion du neurone j à i).
le bridage de cette valeur en utilisant la fonction de transfert. On ramène ainsi toutes la valeur entre 0 et 1. On passe donc le neurone vers un état activé ou désactivé.
l'envoi de cette sortie aux neurones de la couche suivante

Les calculs présentés ci-dessus sont d'ordre général et peuvent s'appliquer à un grand nombre de réseaux.

Architecture de base du réseau

Le principe

L’algorithme de rétro-propagation du gradient est utilisé dans le perceptron multicouche. La phase importante ou ce dernier est utilisé est bien évidemment l’apprentissage.

L'apprentissage

Dans un cadre plus général, l’apprentissage consiste en un entraînement du réseau. On présente au réseau des entrées et on lui demande de modifier sa pondération de telle sorte que l’on retrouve la sortie correspondante. L’algorithme consiste dans un premier temps à propager vers l’avant les entrées jusqu'à obtenir une entrée calculée par le réseau. La seconde étape compare la sortie calculée à la sortie réelle connue. On modifie alors les poids de telle sorte qu’à la prochaine itération, l’erreur commise entre la sortie calculée et connue soit minimisée. Malgré tout, il ne faut pas oublier que l’on a des couches cachées. On rétro-propage alors l’erreur commise vers l’arrière jusqu'à la couche d’entrée tout en modifiant la pondération. On répète ce processus sur tous les exemples jusqu'à temps que l’on obtienne une erreur de sortie considérée comme négligeable.

Un Exemple

Afin de voir un petit peu mieux ce qui se passe considérons un réseau assez simple composé d’une couche d’entrée, une seule couche intermédiaire et une couche de sortie.

On commence tout d’abord les calculs par une initialisation aléatoire des poids. Examinons alors la méthode d’ajustement des poids sur un seul essai :

On calcule les sorties du réseau en fonction de l’entrée du réseau en utilisant les formules de calcul d’activation d’un neurone présentées dans le chapitre précédent.
On calcule les erreurs de chaque neurone à la sortie. Pour calculer cette erreur, on détermine la différence à chaque neurone entre la valeur de sortie calculée et la valeur désirée.

Cette valeur est proportionnelle à la différence de la valeur désirée et calculée et enfin à la dérivée de la fonction de transfert. En effet, plus la pente est forte, plus on doit corriger.

On ajuste les poids vers les neurones de sortie en soustrayant du poids actuel une quantité proportionnelle à l’erreur.

Le nouveau poids se calcule alors en partant de l’ancien poids et en ajoutant une correction proportionnelle d’un côté à l’erreur de l’autre à la valeur reçue de la couche intermédiaire.

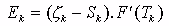
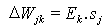
On re-ajuste les poids vers les neurones intermédiaires.

On calcule pour chaque neurone intermédiaire une erreur. Il faut ici que le neurone intermédiaire qui est le plus responsable de l’erreur soit le plus corrigé.

Cette erreur est proportionnelle à la dérivée de la fonction de transfert, car plus la pente est importante, plus il faut corriger. En plus, elle est proportionnelle à la somme pondérée des erreurs de sortie Ainsi, le neurone de sortie ayant le plus gros poids et la plus grosse erreur interviendra le plus dans la correction.

La formule de correction est donc la suivante :

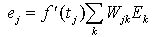
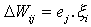
Les notations utilisées sont les suivantes:

La généralisation

L’algorithme de généralisation est très simple dans le sens ou il ne fait qu’une propagation de l’entrée vers l’avant. On ne calcule pas d’erreur étant donné d’une part que la modification doit nous donner « un bon résultat » et d'autre part, que la vraie valeur de sortie n'est pas connue.

L'algorithme

Exemple de structure de données

Le programme proposé est écrit en langage C. La structure utilisée pour coder le réseau est relativement intuitive :

struct neurone

{

float *w; /* Poids des connexions du neurone vers ceux de la couche suivante */

float sortie; /* Sortie du neurone */

float erreur; /*Erreur au neurone */

};

Un neurone est donc une entité comprenant le vecteur des poids vers les neurones de la couche suivante, sa valeur de sortie réelle entre 0 et 1 et enfin l'erreur en rétro-propagation.

Pour modéliser, on peut créer un tableau de neurones tel que:

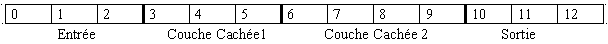
A chaque neurone du tableau on alloue un tableau de poids (w) correspondant aux connexions partants du neurone vers tous les neurones de la couche suivante.

Pour créer un réseau de n neurones, on crée simplement un tableau de n neurones. On s'arrange ensuite pour garder en mémoire la position des couches dans ce tableau.

L'algorithme utilisé

Allocation du réseau

Mise à jour des poids à des valeurs aléatoires

Lecture des exemples d’apprentissage

Faire

Pour chaque exemplaire d’apprentissage Faire

Activation de l’entrée à l’exemple

Propagation de l’entrée vers l’avant

erreur = Calcule l’erreur finale

Propagation de l’erreur vers l’arrière

Ajustement des poids

Mise à jour de l’erreur totale

Fin Pour

Tant que l’erreur totale est supérieure a SEUIL ou le nombre d’itérations inférieur à MAX_ITER

Généralisation sur apprentissage

Propagation de l’entrée vers l’avant

Vérification du résultat avec l’entrée réelle

Lecture du fichier de généralisation

Généralisation

Propagation de l’entrée vers l’avant

Vérification du résultat avec l’entrée réelle

Source du programme en C: Cliquez ici

Résultats

Six bases de données ont été testées en généralisation sur apprentissage avec l’algorithme de rétro-propagation du gradient.


Lenses	Iris	Bupa	Vote	Mushroom	Chess
24 cas	150 cas	345 cas	435 cas	8124 cas	3196 cas
5 entrées	8 entrées	22 entrées	16 entrées	55 entrées	37 entrées
3 sorties	3 sorties	2 sorties	2 sorties	2 sorties	2 sorties

La généralisation sur apprentissage consiste à représenter au réseau les données qu'il a appris. Le résultat doit être normalement de 0% d'erreur si le réseau a effectivement bien appris.

Le premier tableau montre les résultats obtenus sur un réseau mono-couche:

Le tableau suivant montre l'importance de bien choisir le nombre de couches dans son réseau. En effet le raisonnement consistant à dire que plus on met de couche plus le réseau donnera de bons résultats est faux.


Erreur	Lenses	Iris	Bupa	Vote	Mushroom	Chess
0%	.	.	22-5-2	16-5-2	55-5-2	37-5-2
.	.	22-4-2	16-3-2	55-2-2	.	.
0.09%	.	.	.	.	37-2-2	.
0.29%	.	.	22-02	.	.	.
2.67%	.	8-4-3 (75)	.	.	.	.
4.17%	5-3-3	.	.	.	.	.
13%	.	8-4-3 (150)	.	.	.	.

Erreur en fonction de l'architecture du réseau en rétro-propagation

Retour à la page principale.